図形の最大最小問題 2
解答
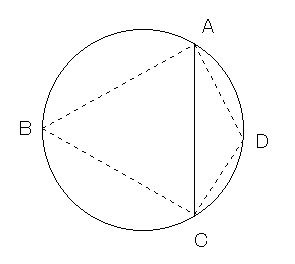
四点をA,B,C,Dとする。
まず、A,Cを固定する
線分ACが図の上下方向になるように、円を回転して差し支えない。
ここで、点AとCを固定し、点BとDを動かして、三角形ABCと三角形ACDの面積が最大にする事を考える。
固定された線分ACを2つの三角形の底辺と見て、点Bと点Dを動かすと、
三角形の面積が最大になるのは、点Bと点Dが、
ACの垂直二等分線(ACの中点を通り、ACに垂直な線)と円との交点にあるときである。
 |
ACを固定した場合には、点Bと点Dが、ACの垂直2等分線と円との交点にあるときに、面積が最大になります |
ここで、
四角形の面積=(ACの長さ)×(⊿ABCの高さ)÷2+(ACの長さ)×(⊿ACDの高さ)÷2
=(ACの長さ)×(円内のACの垂直二等分線の長さ)÷2
=(ACの長さ)×(円の直径)÷2
なので、ACのみに拠る事になります。ここでACを動かします。四角形の面積は、
ACが最大のとき、つまりACが円の直径になっているときです。
なお、ACは横方向(線分BDに垂直を保ったまま)に動かして調べるだけでよいです。
 |
点B,点Cが決定した後にACを動かして、ACが最大になったとき、つまり、ACが直径になっているときに円の面積が最大になります。 |
よって結論は、四角形ABCDが正方形のときに面積は最大になる。